コピペで簡単！ エクセルで離散フーリエ変換、高速フーリエ変換
本項では、エクセルで簡単に実行できる、離散データのフーリエ変換のプログラムを記述してみます。
エクセルのアドイン機能にあるフーリエ変換機能は、計算結果の、実数、虚数が、同じセルに格納されてしまい、
データ解析には使いづらいので、マクロにて実行します。プログラムは、コピーアンド、ペーストで実行できます。
前準備として
単純なフーリエ変換では面白くないので変換後、さらに逆変換を行い、逆変換の時に、任意の次数だけを抽
出する、フーリエフィルターを実装してみます。任意の次数はN次とします。そしてそのN次は、エクセルシート上で
好きな数値で打てるようにします。 また、冒頭のタイトルどおり、離散フーリエ変換と、高速フーリエ変換の、
2種類のプログラムを実装して違いを体感してみましょう。 高速の名は伊達ではありません。 めちゃくちゃ早いですよ。
データ数は4096以上でも出来る！
～前提の条件～
・データ数が多いほど離散フーリエ変換(DFT)と、高速フーリエ変換(FFT)の違いが大きく表れます。 今回は
エクセルのアドイン機能でのフーリエ変換の上限、4096以上のデータ数でも、フーリエ変換が出来るようになってます。
ただし、変換するデータの最大数は倍の8192個をとします。 それ以上は、DFTの計算が凄まじく重くなるのでデータの
変数配列をアドイン解析の出来る倍の8192としました。数値を変えれば増やせますがお勧めできません。
※下手すると固まります
・FFTのアルゴリズムの関係上、データ数は2の乗数でなければ成立しません。 （2,4,8,16,32,64,128,256･･･）
以外のデータを用いる場合は、プログラムエラーになります。
20ギガ 月額￥2980 楽天モバイル ! !
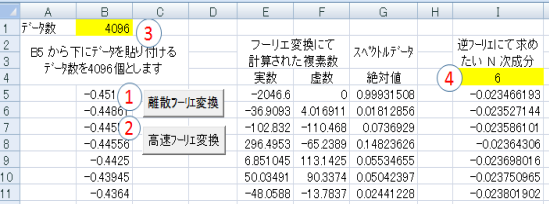
コピペをする前にエクセルシートの準備をします
マクロコードのコピーの前に、 解析を行いたいデータの貼り付け先の準備をしましょう。 準備は、
・①離散フーリエ変換 用のボタン配置
・②高速フーリエ変換 用のボタン配置
・③データ数 の設定
・④逆変換時のN次成分 （1からデータ数の半分で設定）
の4つを配置してましょう。 （配置方法の決まりはありませんが、よく分からない方は、下の写真を参考にしてください）
フーリエ変換を行いたいデータは、B5 セルから縦方向の下に向かって貼り付けて下さい。
マクロコードをコピーしましょう
シート側の準備ができたら、VisualBasicを起動して、対象のシートに、下記のコードを追記します。 写真を参考に、離散フーリエ変換(DFT)と、高速フーリエ変変換のコードを貼り付けましょう。
離散フーリエ変換のコード
関数タイプ、Subとして、DFT_IDFTの名前で作成します。
※ここから↓をコピペします！
Private Sub DFT_IDFT() ' 離散ﾌｰﾘｴ変換
Dim dFr(8192) As Double ' 実数
Dim dFi(8192) As Double ' 虚数
Dim smpl As Integer
Dim Nji As Integer ' 逆変換抽出次数
Dim PI As Double
PI = Atn(1) * 4 ' 3.14
Nji = Cells(4, 9).Value ' 逆変換で求めたい次数
smpl = Cells(1, 2).Value ' ﾃﾞｰﾀ数
' DFT(離散ﾌｰﾘｴ変換)の計算ここから---------------------
For j = 0 To smpl - 1
Fr = 0
Fi = 0
For i = 0 To smpl - 1
Fr = Fr + Cells(5 + i, 2).Value * Cos(2 * PI * i * j / smpl)
Fi = Fi + Cells(5 + i, 2).Value * -Sin(2 * PI * i * j / smpl)
Next
dFr(j) = Fr
dFi(j) = Fi
Cells(10, 3).Value = "DFT計算中"
Cells(11, 3).Value = j
Next
For i = 0 To smpl - 1
Cells(5 + i, 5).Value = dFr(i) '実数結果
Cells(5 + i, 6).Value = dFi(i) '虚数結果
Cells(5 + i, 7).Value = (dFr(i) ^ 2 + dFi(i) ^ 2) ^ 0.5 / (smpl / 2) '絶対値
Next
' DFT の計算ここまで ----------------------------------
' IDFT(離散ﾌｰﾘｴ逆変換)の計算ここから---------------------
For j = 0 To smpl - 1
Fr = 0
For i = 0 To smpl - 1
If (i = Nji) Then ' N次波形の出力
Fr = Fr + (dFr(i) * Cos(2 * PI * i * j / smpl)) - (dFi(i) * Sin(2 * PI * i * j / smpl)) ' N次波形
Else
Fr = Fr + 0 ' それ以外は0でマスク
End If
Next
Cells(5 + j, 9).Value = Fr / (smpl / 2)
Cells(10, 3).Value = "IDFT計算中"
Cells(11, 3).Value = j
Next
' IDFT の計算ここまで
Cells(10, 3).Value = ""
Cells(11, 3).Value = ""
End Sub
高速フーリエ変換のコード
では続いて、FFTのプログラムを、関数タイプ、Subとして、FFT_IFFTの名前で作成します。
※FFTの方だけ、プログラムの効率の為、変換逆変換の処理を同じ関数を通すようにしてますので、
呼び出し元の引数でFFTか、IFFTかを選択できるようにしてます。
※ここから↓をコピペします！
Private Sub FFT_IFFT(Reverse As Integer)
Dim dFr(8192) As Double ' 実数
Dim dFi(8192) As Double ' 虚数
Dim smpl As Integer
Dim Nji As Integer ' 逆変換抽出次数
Dim PI As Double
PI = Atn(1) * 4 ' 3.14
Nji = Cells(4, 9).Value ' 逆変換で求めたい次数
smpl = Cells(1, 2).Value ' ﾃﾞｰﾀ数
Dim c, s, t1, t2, arg, scl As Double
Dim k, lmax, lix, j1, j2, nv2 As Integer
Dim power, flg As Integer
power = Log(smpl) / Log(2) '
scl = 2 * PI / smpl ' 1点当たりの角度(ﾗｼﾞｱﾝ)
lmax = smpl
' 逆FFTの場合はN次以外のﾃﾞｰﾀをﾏｽｸする----------------
If (Reverse = 1) Then
For i = 0 To smpl - 1
If (i = Nji) Then 'N次の波形抽出
dFr(i) = Cells(5 + i, 5).Value 'FFTにて出した実数ﾃﾞｰﾀをｼｰﾄから取り込む
dFi(i) = Cells(5 + i, 6).Value 'FFTにて出した虚数ﾃﾞｰﾀをｼｰﾄから取り込む
Else
dFr(i) = 0
dFi(i) = 0
End If
Next
flg = 1
Else ' FFTでの複素変換
For i = 0 To smpl - 1
dFr(i) = Cells(5 + i, 2).Value ' FFTをするためのﾃﾞｰﾀ計算変数にｾｯﾄする
Next
flg = -1
End If
For i = 0 To power - 1 ' FFT 逆FFT ｱﾙｺﾞﾘｽﾞﾑの真骨頂
lix = lmax ' ﾊﾞﾀﾌﾗｲ演算
lmax = lmax / 2
arg = 0
For j = 0 To lmax - 1
c = Cos(arg)
s = flg * Sin(arg)
arg = arg + scl
For k = lix To smpl
j1 = k - lix + j
j2 = j1 + lmax
t1 = dFr(j1) - dFr(j2)
t2 = dFi(j1) - dFi(j2)
dFr(j1) = dFr(j1) + dFr(j2)
dFi(j1) = dFi(j1) + dFi(j2)
dFr(j2) = (c * t1) + (s * t2)
dFi(j2) = (c * t2) - (s * t1)
k = k + lix
k = k - 1
Next
Next
scl = scl * 2
Next
'bit反転
j = 0
nv2 = smpl / 2
For i = 0 To smpl - 2
If (i ＜ j) Then '※タグ関係上＜は全角なのでペースト時は半角にして下さい
t1 = dFr(j)
t2 = dFi(j)
dFr(j) = dFr(i)
dFi(j) = dFi(i)
dFr(i) = t1
dFi(i) = t2
End If
k = nv2
Do While k ＜ (j + 1) '※ここも＜は全角なので注意して下さい
j = j - k
k = k / 2
Loop
j = j + k
Next
If (flg = 1) Then ' FFT逆変換
For i = 0 To smpl - 1
Cells(5 + i, 9).Value = dFr(i) / (smpl/2) ' N次波形の出力
Next
Else ' FFT変換
Cells(5, 5).Value = dFr(0)
For i = 1 To smpl - 1
Cells(5 + i, 5).Value = dFr(i) '実数ﾃﾞｰﾀ
Cells(5 + i, 6).Value = dFi(i) '虚数ﾃﾞｰﾀ
Next
End If
End Sub
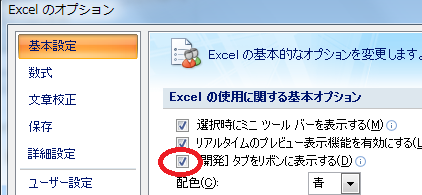
まって、Visual Basic のタブが無い！
はじめてマクロを使われる方は、恐らくVBのリボンが無いと思われるので、設定プロパティより、開発タブを 追加してVBを選べるように設定しましょう。 下記の写真を参考に、開発タブを追加しましょう。
コードのコピーが出来たら、ボタンのイベントを追加しましょう
マクロコードの準備が出来たら、ボタンイベントから、フーリエ変換の、関数を呼べるようにしましょう。 デザインで配置したボタンがあれば、下記写真のように、CommandButton1,2が出てくるはずなので、 それぞれをクリックしてイベント関数を追加します。
ボタンの関数が出来たら、下の写真を参考に、先ほど作成したプログラムを呼び出せるよう追記します。
エクセルシートから、ボタンを押して、プログラムを実行してみましょう
ではいよいよ、マクロを実行してみましょう。
どうでしたか？ うまくできましたか？
マクロが実行されると、E,F,G列に、フーリエ変換結果、I位列に逆変換時の結果が、出力されると思います。 変換対象のデータ（B列のデータ）と変換後のデータ（I列のデータ）を、散布図のグラフ表示を使って表示 して比較してみましょう。
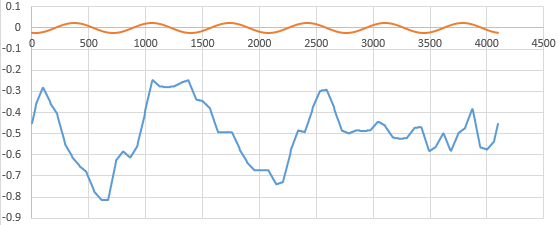
変換対象のデータ(B列のデータ)が水色波形で、変換後のデータ（I列のデータ）がオレンジ色です。
変換後のデータは、④のN次で設定した6周期のsin波形がになるはずです。
変換結果の値が正しいか不安な方は、エクセルのデータ解析タブ内に
ある、フーリエ解析機能を使って、同じデータのフーリエ変換を実施してみましょう。
結果のデータが同じでればOKです。
※ただし、FFTの場合、アルゴリズムの関係上、虚数側のデータの極性が逆になります。また、0次成分(0周波数)
を含めたフィルター処理なしの、逆変換を行う場合、結果を/N個データ数で割る、式が若干変わってきます。
より詳細な勉強がしたい方は、
Excelではじめるディジタル信号処理
いかがだったでしょうか？ FFTの計算は今や至る所で使われていますのね。 次は、エクセルで出来る FIRフィルタのプログラム例をコーディングをしてみようと思います。 ※現在工事中です
最新のドラマ、アニメが31日間無料視聴できる！
こんなのあったんだ！がきっと見つかる
chosyoshinsya 2015～2019 All Rights Reserved.
